Landmarks defining transforms
Gregory Jefferis
2020-06-08
Source:vignettes/landmarks.Rmd
landmarks.RmdIntro
One of the core features of elmr is to enable data in the FAFB EM space to be transformed into one of a number of standard light level template brains. This transformation depends on manually selected landmarks. We can inspect these landmarks and to try to measure their consistency.
Setup
library(elmr) library(knitr) opts_chunk$set(fig.width=5, fig.height=5) # set up for 3d plots based on rgl package rgl::setupKnitr() # frontal view view3d(userMatrix=rgl::rotationMatrix(angle = pi, 1,0,0), zoom=0.7)
Landmarks
The standard landmarks used by elmr were specified by Davi Bock on the FAFB and JFRC2013 brains using the elm tool developed by Stefan Saalfeld and John Bogovic. We can plot the landmarks in the context of the JFRC2013 brain as follows.
plot3d(JFRC2013) # note that the landmarks are in raw voxel coordinates and must be scaled xyz=scale(elm.landmarks[,c("X","Y","Z")], scale = 1/voxdims(JFRC2013), center = FALSE) xyz=as.data.frame(xyz) rownames(xyz)=sub("Pt-","",elm.landmarks$Label) spheres3d(xyz, col = ifelse(elm.landmarks$Use, "green", 'red'), radius = 4)
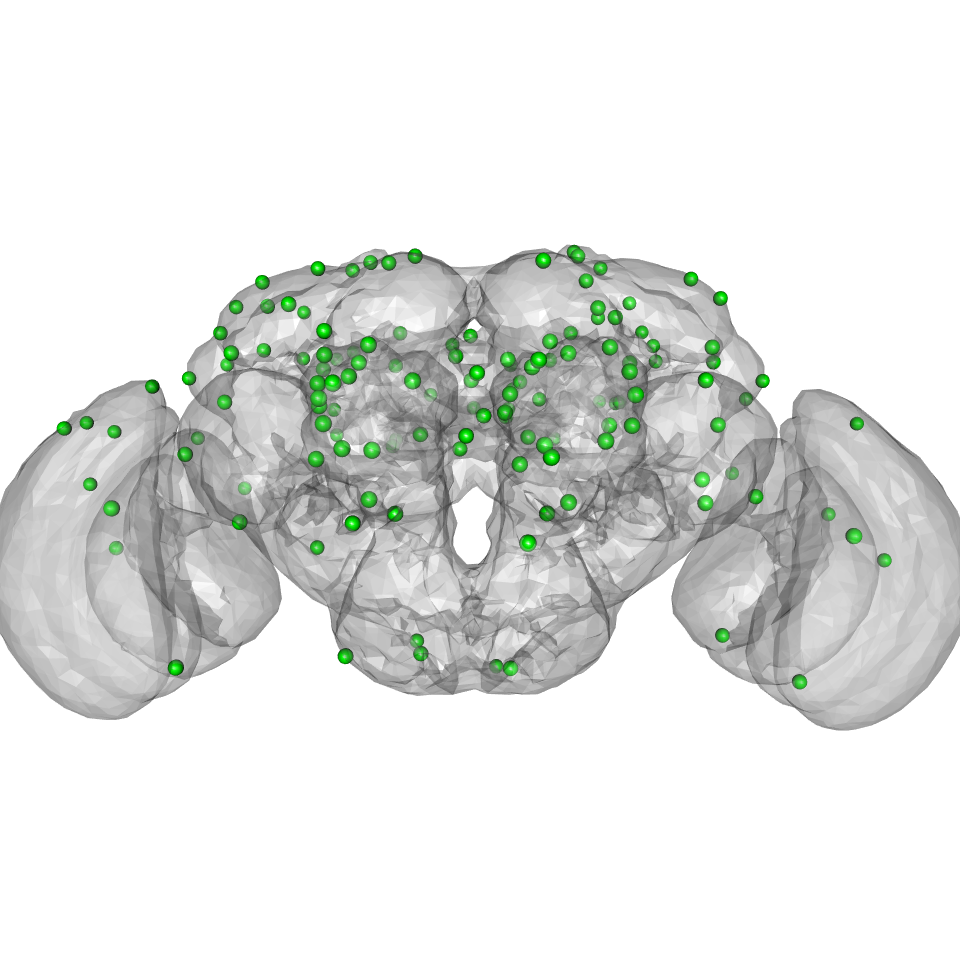
Landmarks based transform
The standard elm.landmarks set is used within to the elmr package to register a transformation that can map FAFB->JFRC2013 space in conjunction with the xform_brain functions provided by the nat.templatebrains packages.
Let’s first look at the FAFB landmarks
# note that these positions are in nm units and do not need scaling xyz.fafb=elm.landmarks[,c("X1","Y1","Z1")] rownames(xyz.fafb)=sub("Pt-","",elm.landmarks$Label) kable(head(xyz.fafb))
| X1 | Y1 | Z1 | |
|---|---|---|---|
| 1 | 452638.6 | 93129.93 | 92560 |
| 2 | 522271.2 | 184057.51 | 96160 |
| 3 | 428701.7 | 173888.16 | 112440 |
| 6 | 597973.7 | 99741.26 | 77200 |
| 7 | 629661.1 | 172401.93 | 146120 |
| 8 | 629608.0 | 170950.13 | 185640 |
Now we can try to look at the consistency of the transform between each landmark pair as follows:
- Drop out each landmark pair in turn
- Calculate position of that landmark in target space using remaining landmark pairs
- Measure difference between calculated position and manually defined position
# record transformed position with leave one out xyzt.loo=xyz for(i in 1:nrow(xyz)) { thisreg <- reglist(tpsreg(xyz.fafb[-i, ], xyz[-i, ])) xyzt.loo[i,]=xform(xyz.fafb[i, , drop=FALSE], thisreg) } deltas=sqrt(rowSums((xyzt.loo-xyz)^2)) hist(deltas)
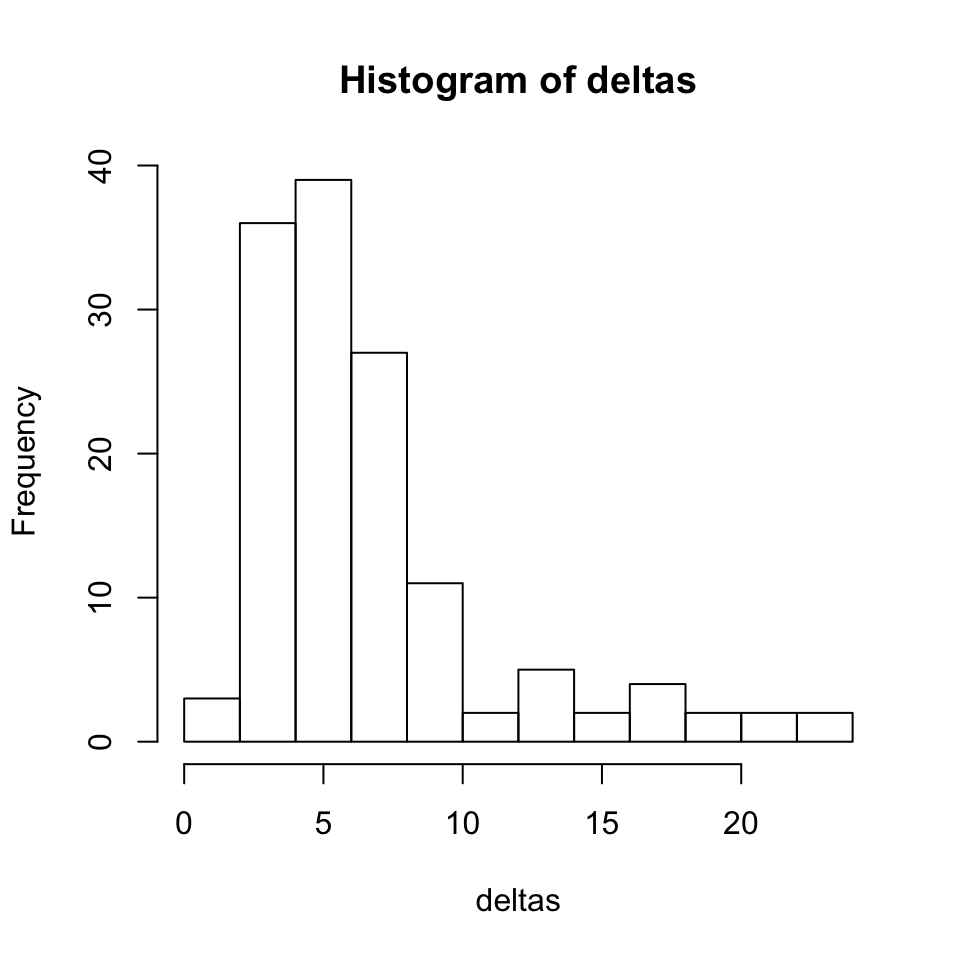
Let’s looks at the deltas (distance between leave one out vs manually defined landmark position) for each point.
| Label | Use | X | Y | Z | X1 | Y1 | Z1 | delta | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Pt-1 | TRUE | 571.4001 | 38.85996 | 287.05954 | 452638.6 | 93129.93 | 92560 | 4.8567731 |
| 2 | Pt-2 | TRUE | 715.8113 | 213.29936 | 217.39349 | 522271.2 | 184057.51 | 96160 | 2.0271878 |
| 3 | Pt-3 | TRUE | 513.0022 | 198.00197 | 217.79409 | 428701.7 | 173888.16 | 112440 | 8.6873515 |
| 6 | Pt-6 | TRUE | 867.0125 | 31.91925 | 276.22344 | 597973.7 | 99741.26 | 77200 | 4.5722904 |
| 7 | Pt-7 | TRUE | 935.2109 | 234.22952 | 351.51807 | 629661.1 | 172401.93 | 146120 | 6.6747676 |
| 8 | Pt-8 | TRUE | 935.2109 | 232.62607 | 405.50079 | 629608.0 | 170950.13 | 185640 | 6.4982959 |
| 10 | Pt-10 | TRUE | 509.7629 | 244.91917 | 362.20772 | 431157.3 | 165611.08 | 169920 | 8.8340362 |
| 11 | Pt-11 | TRUE | 509.2284 | 281.12828 | 403.48102 | 431024.0 | 173148.67 | 207560 | 5.1295757 |
| 12 | Pt-12 | TRUE | 509.2284 | 165.87835 | 401.67082 | 431057.1 | 125923.99 | 189520 | 6.7021690 |
| 14 | Pt-14 | TRUE | 1106.8503 | 372.72023 | 222.01044 | 711682.1 | 254995.10 | 112320 | 12.4510042 |
| 17 | Pt-17 | TRUE | 718.4719 | 242.59406 | 355.69466 | 531137.1 | 165586.38 | 164680 | 2.6243835 |
| 18 | Pt-18 | TRUE | 776.9947 | 213.33267 | 378.56799 | 566543.7 | 148578.85 | 171000 | 8.3093447 |
| 19 | Pt-19 | TRUE | 839.6388 | 287.10433 | 382.68932 | 587828.7 | 180069.25 | 180880 | 6.0548760 |
| 20 | Pt-20 | TRUE | 601.2203 | 288.54680 | 382.68932 | 479270.4 | 176726.32 | 190640 | 2.5302671 |
| 21 | Pt-21 | TRUE | 653.3550 | 221.57531 | 380.62865 | 500660.6 | 148115.02 | 175520 | 3.1633781 |
| 23 | Pt-23 | TRUE | 646.4883 | 588.60129 | 222.43882 | 502568.4 | 335377.59 | 185680 | 14.3595881 |
| 24 | Pt-24 | TRUE | 769.5130 | 605.94266 | 204.25736 | 555571.9 | 350062.58 | 171760 | 2.9367527 |
| 25 | Pt-25 | TRUE | 1150.4870 | 201.70284 | 365.00699 | 733410.6 | 150225.52 | 148840 | 8.2068118 |
| 26 | Pt-26 | TRUE | 1045.9179 | 168.05378 | 215.08408 | 685711.4 | 174524.46 | 68960 | 3.0133531 |
| 27 | Pt-27 | TRUE | 389.1564 | 177.03002 | 206.10784 | 369059.9 | 163273.69 | 105480 | 4.8117727 |
| 39 | Pt-39 | TRUE | 294.9652 | 198.55742 | 355.90246 | 324455.5 | 140507.97 | 176320 | 5.7458094 |
| 40 | Pt-40 | TRUE | 241.6744 | 211.20539 | 350.83541 | 301541.1 | 160802.95 | 176320 | 7.4296983 |
| 45 | Pt-45 | TRUE | 325.9132 | 597.71786 | 158.23298 | 340429.1 | 338520.68 | 171320 | 20.7364915 |
| 46 | Pt-46 | TRUE | 197.7791 | 449.11545 | 319.63260 | 306709.7 | 285779.48 | 222520 | 22.7770038 |
| 47 | Pt-47 | TRUE | 120.6732 | 274.52403 | 323.29304 | 233960.2 | 216887.97 | 181080 | 15.5495428 |
| 48 | Pt-48 | TRUE | 162.5141 | 275.24054 | 425.51338 | 285325.0 | 165261.48 | 232120 | 16.4094093 |
| 49 | Pt-49 | TRUE | 413.3632 | 161.16906 | 316.82330 | 382965.0 | 139994.70 | 148000 | 4.9865533 |
| 51 | Pt-51 | TRUE | 732.8606 | 262.06885 | 208.87088 | 532888.7 | 206000.44 | 102280 | 2.8474895 |
| 52 | Pt-52 | TRUE | 763.4152 | 262.35759 | 225.77664 | 549393.3 | 198858.96 | 104640 | 5.8249803 |
| 56 | Pt-56 | TRUE | 1021.5445 | 379.96095 | 136.36467 | 669071.4 | 282885.13 | 73560 | 3.9146401 |
| 57 | Pt-57 | TRUE | 1212.4784 | 422.50773 | 128.28765 | 744107.8 | 289188.76 | 100560 | 19.2798860 |
| 58 | Pt-58 | TRUE | 1249.0229 | 401.20869 | 365.68265 | 756760.4 | 233828.39 | 201200 | 3.8537199 |
| 59 | Pt-59 | TRUE | 1174.4594 | 631.83024 | 248.45789 | 745417.8 | 353730.87 | 198160 | 22.6614828 |
| 60 | Pt-60 | TRUE | 1077.1313 | 573.66563 | 299.84596 | 674374.9 | 325483.14 | 198160 | 17.6697144 |
| 61 | Pt-61 | TRUE | 1112.7070 | 339.48705 | 401.72907 | 683073.3 | 207169.29 | 198160 | 19.3194897 |
| 62 | Pt-62 | TRUE | 1306.1523 | 263.30353 | 411.07188 | 786547.0 | 167538.31 | 198160 | 7.2968528 |
| 63 | Pt-63 | TRUE | 1328.8859 | 469.20296 | 354.47855 | 786667.9 | 254601.10 | 219560 | 12.1283499 |
| 64 | Pt-64 | TRUE | 549.6954 | 583.20048 | 162.32429 | 436921.0 | 324144.32 | 168120 | 13.3160542 |
| 65 | Pt-65 | TRUE | 765.1116 | 188.70754 | 178.33252 | 543563.4 | 191829.65 | 66480 | 7.0929336 |
| 66 | Pt-66 | TRUE | 785.3950 | 425.64347 | 15.25080 | 559862.1 | 319733.97 | 42880 | 7.2362758 |
| 67 | Pt-67 | TRUE | 491.9622 | 447.69119 | 309.37694 | 416087.8 | 250364.48 | 202160 | 4.3195663 |
| 68 | Pt-68 | TRUE | 636.6000 | 582.23100 | 304.45079 | 475821.1 | 301542.34 | 209200 | 17.8857285 |
| 69 | Pt-69 | TRUE | 751.5368 | 622.07216 | 324.54432 | 549630.2 | 318599.41 | 227360 | 11.0236700 |
| 70 | Pt-70 | TRUE | 248.6964 | 386.77664 | 133.64117 | 302955.0 | 281032.97 | 132480 | 12.9435630 |
| 71 | Pt-71 | TRUE | 371.3233 | 241.13746 | 246.95856 | 352159.8 | 181155.82 | 132480 | 5.6993404 |
| 72 | Pt-72 | TRUE | 125.3698 | 356.45723 | 424.67776 | 276788.0 | 219417.40 | 262680 | 16.6889349 |
| 74 | Pt-74 | TRUE | 297.1745 | 286.05935 | 401.86582 | 328376.8 | 172800.07 | 224200 | 12.3145756 |
| 75 | Pt-75 | TRUE | 120.6515 | 261.44368 | 422.62512 | 234767.8 | 172806.20 | 231640 | 20.4604900 |
| 76 | Pt-76 | TRUE | 371.7625 | 362.30048 | 386.60631 | 372970.9 | 200278.04 | 221400 | 9.9392250 |
| 77 | Pt-77 | TRUE | 863.6581 | 20.51800 | 305.28403 | 593593.3 | 92800.43 | 83480 | 5.2978426 |
| 78 | Pt-78 | TRUE | 877.3450 | 69.27787 | 262.22208 | 602858.0 | 116568.92 | 72080 | 4.9387303 |
| 79 | Pt-79 | TRUE | 887.6924 | 116.68930 | 198.29597 | 610278.8 | 156940.02 | 53160 | 4.1762134 |
| 80 | Pt-80 | TRUE | 456.7993 | 163.75185 | 410.38070 | 413853.6 | 120770.68 | 191640 | 4.8779902 |
| 81 | Pt-81 | TRUE | 457.2808 | 92.26043 | 414.81480 | 413799.3 | 90902.71 | 166320 | 8.3478615 |
| 82 | Pt-82 | TRUE | 543.1608 | 46.12096 | 309.74346 | 441965.7 | 86907.20 | 110360 | 2.2727861 |
| 83 | Pt-83 | TRUE | 610.5969 | 134.29354 | 334.08200 | 475282.3 | 125516.26 | 138120 | 3.3060558 |
| 84 | Pt-84 | TRUE | 687.3255 | 150.56257 | 339.67920 | 517256.1 | 128105.25 | 138120 | 5.0033435 |
| 85 | Pt-85 | TRUE | 637.3402 | 37.40585 | 246.20518 | 485233.0 | 96212.32 | 71640 | 6.9772825 |
| 86 | Pt-86 | TRUE | 601.4145 | 48.82580 | 235.55270 | 457888.0 | 104535.82 | 71560 | 7.5135967 |
| 87 | Pt-87 | TRUE | 470.4498 | 113.37605 | 185.97815 | 412043.1 | 138743.20 | 73360 | 9.7471167 |
| 88 | Pt-88 | TRUE | 646.9302 | 287.95844 | 201.12036 | 497269.3 | 219264.50 | 105080 | 6.8055324 |
| 89 | Pt-89 | TRUE | 617.9160 | 393.59540 | 128.45568 | 479040.7 | 271503.39 | 106320 | 7.1815581 |
| 90 | Pt-90 | TRUE | 539.2479 | 159.18572 | 362.26769 | 448664.2 | 130197.79 | 162440 | 3.6823690 |
| 91 | Pt-91 | TRUE | 599.1029 | 299.87976 | 339.71151 | 475916.7 | 189951.39 | 167480 | 4.0787974 |
| 92 | Pt-92 | TRUE | 524.0257 | 228.59402 | 80.51068 | 429789.2 | 217571.25 | 44040 | 4.5038170 |
| 94 | Pt-94 | TRUE | 568.7742 | 195.81066 | 147.47252 | 447827.5 | 191431.30 | 65080 | 7.1549798 |
| 95 | Pt-95 | TRUE | 559.2319 | 216.64859 | 115.06092 | 451509.5 | 210571.92 | 56680 | 2.0295053 |
| 96 | Pt-96 | TRUE | 694.7296 | 181.04882 | 208.66967 | 512860.3 | 173756.69 | 83760 | 3.7317246 |
| 97 | Pt-97 | TRUE | 522.7734 | 153.64999 | 152.36817 | 424630.5 | 170571.37 | 65520 | 6.4315287 |
| 98 | Pt-98 | TRUE | 723.9280 | 208.76311 | 156.20774 | 521821.9 | 191059.99 | 65920 | 9.4240092 |
| 99 | Pt-99 | TRUE | 561.4849 | 406.58976 | 139.86903 | 439456.2 | 277536.72 | 114040 | 8.7170864 |
| 102 | Pt-102 | TRUE | 589.7660 | 374.11829 | 65.80798 | 456343.4 | 278586.81 | 70040 | 5.4709799 |
| 104 | Pt-104 | TRUE | 528.9954 | 249.36157 | 52.77704 | 429666.7 | 236504.64 | 40720 | 2.6290145 |
| 105 | Pt-105 | TRUE | 559.3112 | 311.49054 | 38.99692 | 446608.2 | 266996.18 | 40720 | 4.4235895 |
| 106 | Pt-106 | TRUE | 536.0237 | 280.85395 | 42.25106 | 428356.2 | 251917.06 | 39440 | 3.6249780 |
| 108 | Pt-108 | TRUE | 529.8430 | 190.66314 | 99.95127 | 443220.7 | 198582.95 | 46960 | 8.8340324 |
| 109 | Pt-109 | TRUE | 588.3022 | 180.80908 | 73.79142 | 465835.1 | 208589.43 | 30640 | 3.2212746 |
| 110 | Pt-110 | TRUE | 523.6692 | 255.82408 | 96.18389 | 432486.9 | 227589.09 | 60560 | 2.0600276 |
| 111 | Pt-111 | TRUE | 519.9193 | 323.34459 | 95.62596 | 429673.5 | 249409.19 | 75440 | 5.6314508 |
| 112 | Pt-112 | TRUE | 644.9661 | 227.95424 | 49.43940 | 492185.1 | 238768.76 | 27200 | 4.9893856 |
| 114 | Pt-114 | TRUE | 596.8888 | 313.78083 | 28.38294 | 467809.3 | 269292.47 | 39960 | 3.9160562 |
| 115 | Pt-115 | TRUE | 549.6726 | 232.40734 | 27.72951 | 435030.4 | 233285.12 | 26120 | 5.8291358 |
| 116 | Pt-116 | TRUE | 793.1537 | 291.40008 | 203.01114 | 552445.9 | 221911.47 | 96760 | 7.4515988 |
| 117 | Pt-117 | TRUE | 932.0076 | 190.30624 | 207.65353 | 623021.1 | 182913.48 | 78400 | 6.3006672 |
| 118 | Pt-118 | TRUE | 913.0380 | 127.35328 | 214.32475 | 619919.5 | 154904.04 | 69920 | 4.0765125 |
| 119 | Pt-119 | TRUE | 1049.5826 | 275.41781 | 194.25617 | 678227.0 | 226038.51 | 77000 | 3.8476223 |
| 121 | Pt-121 | TRUE | 778.8555 | 329.78345 | 110.36329 | 553018.5 | 264730.38 | 62080 | 2.3813873 |
| 122 | Pt-122 | TRUE | 766.8180 | 238.30891 | 129.28220 | 546434.1 | 223179.57 | 44560 | 5.3464239 |
| 126 | Pt-126 | TRUE | 821.1940 | 165.31615 | 170.20768 | 580468.1 | 184025.15 | 57240 | 5.6133324 |
| 127 | Pt-127 | TRUE | 814.9952 | 231.24334 | 335.40372 | 568773.4 | 173760.52 | 141240 | 9.5395721 |
| 128 | Pt-128 | TRUE | 988.4672 | 148.08581 | 377.28153 | 658380.7 | 134538.09 | 155240 | 2.8092561 |
| 129 | Pt-129 | TRUE | 991.9385 | 171.66403 | 374.07560 | 658486.8 | 144747.32 | 155240 | 0.8946411 |
| 130 | Pt-130 | TRUE | 955.0846 | 81.15812 | 394.58469 | 644408.4 | 104909.96 | 146160 | 3.3820125 |
| 131 | Pt-131 | TRUE | 858.8542 | 137.36019 | 305.95222 | 585811.2 | 138028.77 | 109960 | 7.9843254 |
| 132 | Pt-132 | TRUE | 902.7680 | 109.49854 | 349.66070 | 616437.7 | 117813.37 | 130960 | 3.7968063 |
| 133 | Pt-133 | TRUE | 1063.1324 | 180.50395 | 294.78720 | 693213.5 | 164460.49 | 113480 | 1.2879857 |
| 139 | Pt-139 | TRUE | 1031.4633 | 60.62717 | 298.21962 | 685748.2 | 117615.93 | 97360 | 4.0234049 |
| 140 | Pt-140 | TRUE | 1072.7554 | 89.46014 | 292.45409 | 702673.0 | 128121.18 | 103640 | 4.5195348 |
| 141 | Pt-141 | TRUE | 906.2379 | 36.43737 | 347.67361 | 617878.2 | 90004.29 | 110640 | 1.1635802 |
| 142 | Pt-142 | TRUE | 894.3160 | 179.67182 | 111.32961 | 611880.8 | 221748.47 | 22560 | 5.9632264 |
| 143 | Pt-143 | TRUE | 806.9353 | 307.39564 | 41.45364 | 563795.2 | 280366.60 | 24360 | 3.5135552 |
| 144 | Pt-144 | TRUE | 840.9156 | 187.58365 | 109.41779 | 586630.0 | 218165.18 | 24360 | 2.8986408 |
| 145 | Pt-145 | TRUE | 882.2956 | 302.07558 | 46.33199 | 604025.1 | 281980.35 | 24360 | 3.5220758 |
| 146 | Pt-146 | TRUE | 918.1660 | 212.11489 | 98.60478 | 619392.5 | 233507.39 | 21320 | 3.0237052 |
| 147 | Pt-147 | TRUE | 895.6440 | 278.92859 | 131.98689 | 612176.8 | 239146.97 | 56800 | 6.1187261 |
| 148 | Pt-148 | TRUE | 760.4791 | 261.92395 | 138.44280 | 544916.4 | 238404.45 | 56800 | 6.9567334 |
| 150 | Pt-150 | TRUE | 1019.6740 | 349.16788 | 149.33955 | 664468.4 | 266903.26 | 65720 | 6.3876473 |
| 151 | Pt-151 | TRUE | 920.9986 | 280.81417 | 97.82217 | 627242.5 | 257156.22 | 39080 | 5.5171652 |
| 152 | Pt-152 | TRUE | 921.7953 | 243.70019 | 69.01316 | 618928.3 | 257152.53 | 15920 | 4.8130192 |
| 153 | Pt-153 | TRUE | 1026.1469 | 218.11495 | 158.36097 | 669259.1 | 208512.87 | 46280 | 4.7513239 |
| 154 | Pt-154 | TRUE | 815.5029 | 393.53224 | 138.96906 | 569609.9 | 281005.27 | 90880 | 2.9149836 |
| 155 | Pt-155 | TRUE | 794.5535 | 205.37576 | 107.90936 | 568153.1 | 215132.53 | 29160 | 5.2031648 |
| 156 | Pt-156 | TRUE | 801.2243 | 199.57122 | 76.64452 | 568700.7 | 225895.95 | 10560 | 2.6632709 |
| 158 | Pt-158 | TRUE | 814.9698 | 322.09382 | 38.20410 | 568697.9 | 283356.34 | 29360 | 2.4646616 |
| 159 | Pt-159 | TRUE | 838.3869 | 377.84149 | 71.16519 | 583877.6 | 290936.45 | 63640 | 7.0485530 |
| 160 | Pt-160 | TRUE | 411.8688 | 62.66130 | 313.62719 | 394760.5 | 91104.42 | 119360 | 10.7763448 |
| 161 | Pt-161 | TRUE | 496.8204 | 48.48879 | 281.87705 | 417463.3 | 91287.59 | 105160 | 7.6300593 |
| 162 | Pt-162 | TRUE | 428.9324 | 105.46846 | 259.46298 | 387742.4 | 120397.12 | 112400 | 5.6982507 |
| 163 | Pt-163 | TRUE | 348.1907 | 135.07246 | 325.80300 | 351378.7 | 120400.07 | 153960 | 5.0459193 |
| 164 | Pt-164 | TRUE | 709.1743 | 290.44481 | 186.96499 | 519852.8 | 220066.31 | 101920 | 4.1074545 |
| 165 | Pt-165 | TRUE | 699.9468 | 306.79750 | 238.26757 | 521274.8 | 208667.13 | 125880 | 6.2903583 |
| 166 | Pt-166 | TRUE | 608.1120 | 187.71150 | 274.79127 | 471356.9 | 156196.13 | 119480 | 3.4605347 |
| 167 | Pt-167 | TRUE | 714.0975 | 140.92095 | 311.99102 | 520683.3 | 131647.18 | 119480 | 4.2230713 |
| 168 | Pt-168 | TRUE | 772.3868 | 182.61529 | 314.80399 | 549523.6 | 144648.80 | 128720 | 5.7080171 |
| 169 | Pt-169 | TRUE | 768.2635 | 248.16935 | 300.42741 | 549526.6 | 181341.05 | 139520 | 3.3483182 |
| 170 | Pt-170 | TRUE | 826.6157 | 180.43207 | 267.93905 | 581265.9 | 162330.58 | 105360 | 6.2424722 |
| 171 | Pt-171 | TRUE | 785.7634 | 208.03504 | 306.12177 | 560689.1 | 163361.97 | 133400 | 5.3466226 |
| 172 | Pt-172 | TRUE | 811.7054 | 59.21032 | 162.54342 | 566206.7 | 134796.13 | 28680 | 5.0805028 |
| 173 | Pt-173 | TRUE | 322.4938 | 314.56546 | 221.63341 | 326640.0 | 225641.20 | 141360 | 6.3571177 |
| 174 | Pt-174 | TRUE | 405.4023 | 406.32913 | 182.38558 | 370744.3 | 267765.51 | 141360 | 3.4199451 |
| 175 | Pt-175 | TRUE | 370.4399 | 96.40938 | 329.08686 | 365886.3 | 100756.18 | 138560 | 3.5423043 |
| 176 | Pt-176 | TRUE | 912.5393 | 228.67122 | 427.44708 | 621995.4 | 159644.05 | 202720 | 5.2879125 |
| 177 | Pt-177 | TRUE | 976.2923 | 123.25038 | 411.18404 | 646015.3 | 122117.82 | 165280 | 7.0213588 |
| 178 | Pt-178 | TRUE | 1129.1425 | 227.70428 | 380.81028 | 722705.1 | 167172.74 | 162120 | 7.7402841 |
| 179 | Pt-179 | TRUE | 341.2364 | 173.62318 | 404.95490 | 351948.7 | 124957.93 | 194040 | 3.4439352 |
And then visualise them in 3D, colouring each point by the magnitude of the delta.
clear3d() view3d(userMatrix=rgl::rotationMatrix(angle = pi, 1,0,0), zoom=0.7) jet.colors <- colorRampPalette(c("#00007F", "blue", "#007FFF", "cyan", "#7FFF7F", "yellow", "#FF7F00", "red", "#7F0000")) plot3d(JFRC2013) spheres3d(xyz, col = jet.colors(10)[cut(deltas, 10)], radius = 4) # nb these are numbered from 0 like the elm landmarks texts3d(xyz, texts = rownames(xyz), adj = c(1,1))
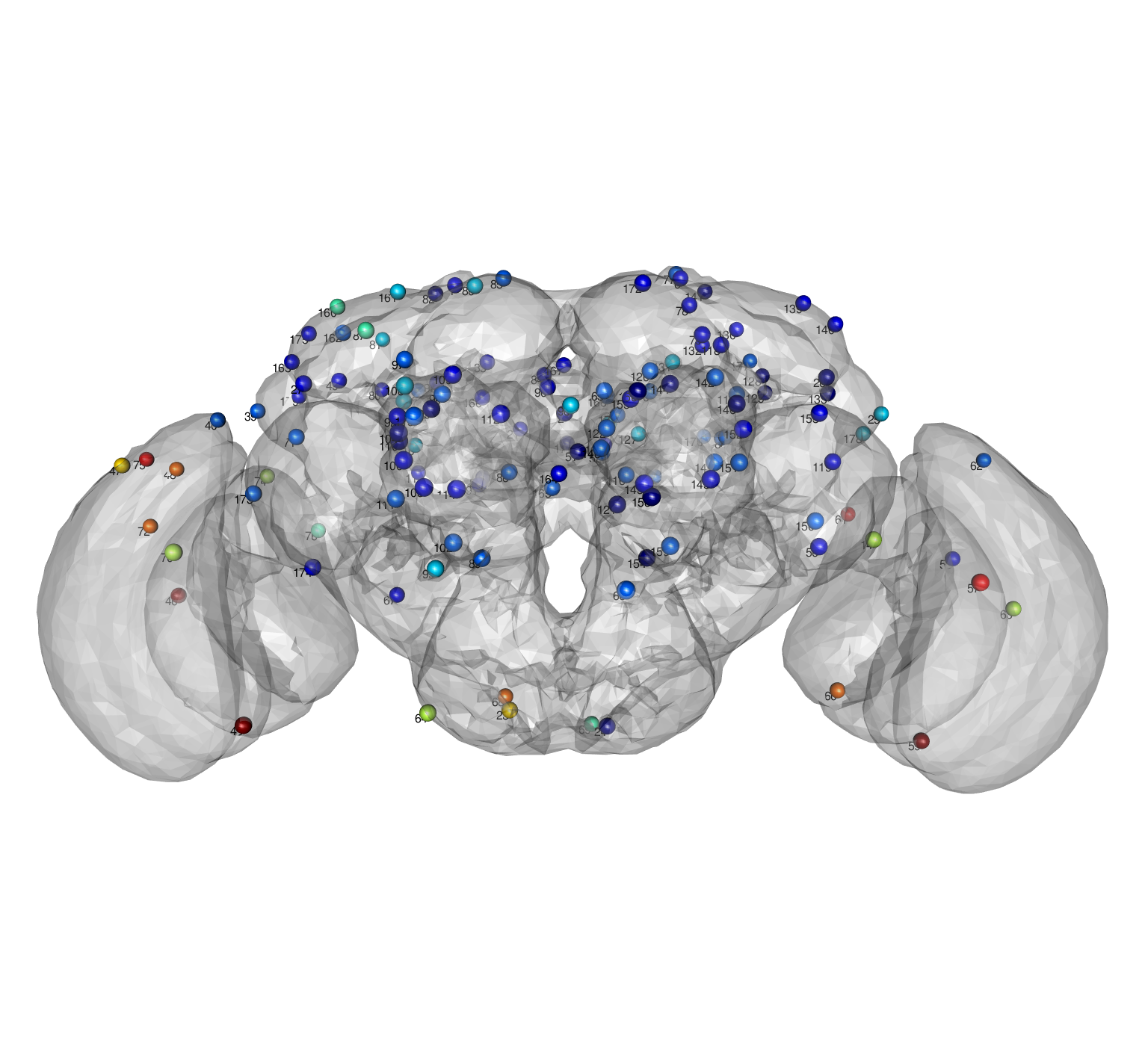
Based on this, I would definitely suggest checking the following landmarks
75/48 43 46 68 23
Compare the leave one out landmark position with manually defined position
clear3d() view3d(userMatrix=rgl::rotationMatrix(angle = pi, 1,0,0), zoom=0.7) for(i in 1:nrow(xyz)){ segments3d(rbind(xyz[i, , drop=FALSE], xyzt.loo[i, , drop=FALSE]), col=jet.colors(10)[cut(deltas, 10)][i], lwd=3) } points3d(xyz) texts3d(xyz, texts = rownames(xyz), adj = c(1,1)) plot3d(JFRC2013)
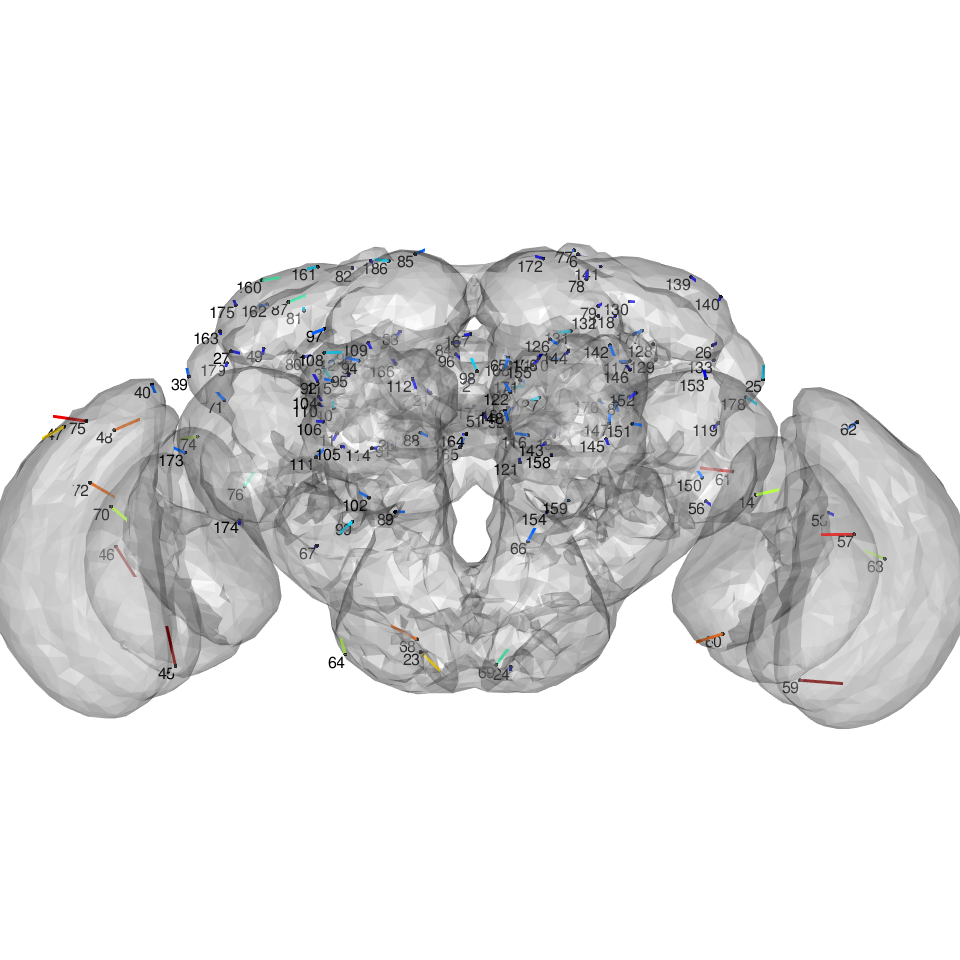
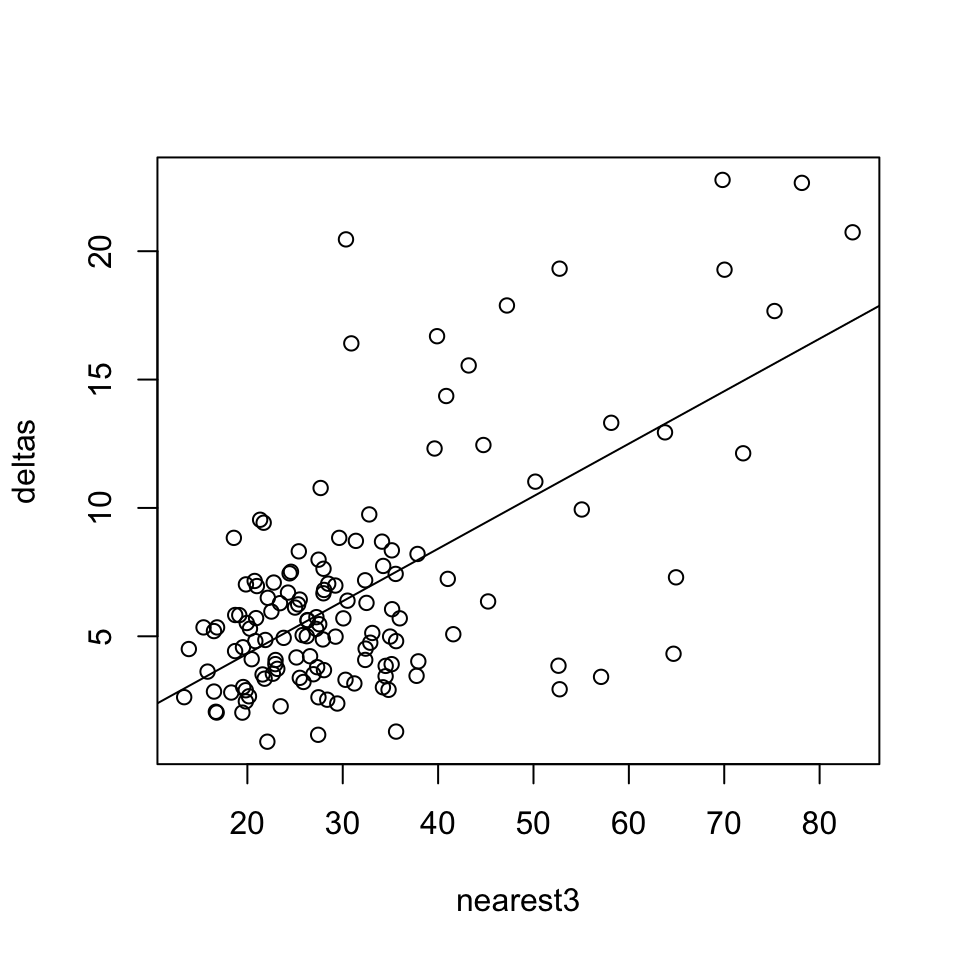
Now of course this is not just a measure of consistency in each landmark point, but it will also depend strongly on the extent to which the neighbouring points can define the required registration; in areas requiring substantial non-rigid deformation this may be a problem; this will be further emphasised when the neighbouring points are distant. We can check the latter point like so:
library(nabor) nearest3=rowMeans(nabor::knn(xyz, k=4)$nn.dists[,-1]) plot(deltas~nearest3) deltabynearest3=lm(deltas~nearest3) abline(deltabynearest3)
summary(deltabynearest3)
##
## Call:
## lm(formula = deltas ~ nearest3)
##
## Residuals:
## Min 1Q Median 3Q Max
## -9.1418 -2.0414 -0.1602 1.6765 14.0253
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.22861 0.74626 0.306 0.76
## nearest3 0.20458 0.02155 9.491 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.522 on 133 degrees of freedom
## Multiple R-squared: 0.4038, Adjusted R-squared: 0.3993
## F-statistic: 90.08 on 1 and 133 DF, p-value: < 2.2e-16So there is a correlation between neighbour distance and our calculated delta; with an R^2 of about 0.4 it’s reasonably strong. This may be explained by Davi placing more landmarks in areas where he is more certain.
Perhaps the ideal thing would be to find a set of landmarks on one side of the brain and then find exactly the same landmarks on the other side of the brain. For the JFRC2013 brain we can exactly mirror points from one side to the other using an image-based registration distributed with the nat.flybrains package.
We can find the mirror image position of all the points that we used like so:
# nb this is conditioned on being able to find CMTK if(isTRUE(nzchar(cmtk.bindir()))){ xyzm=mirror_brain(xyz, brain = JFRC2013) clear3d() spheres3d(xyz, col='red', rad=2) spheres3d(xyzm, col='green', rad=2) plot3d(JFRC2013) view3d(userMatrix=rgl::rotationMatrix(angle = pi, 1,0,0), zoom=0.7) }
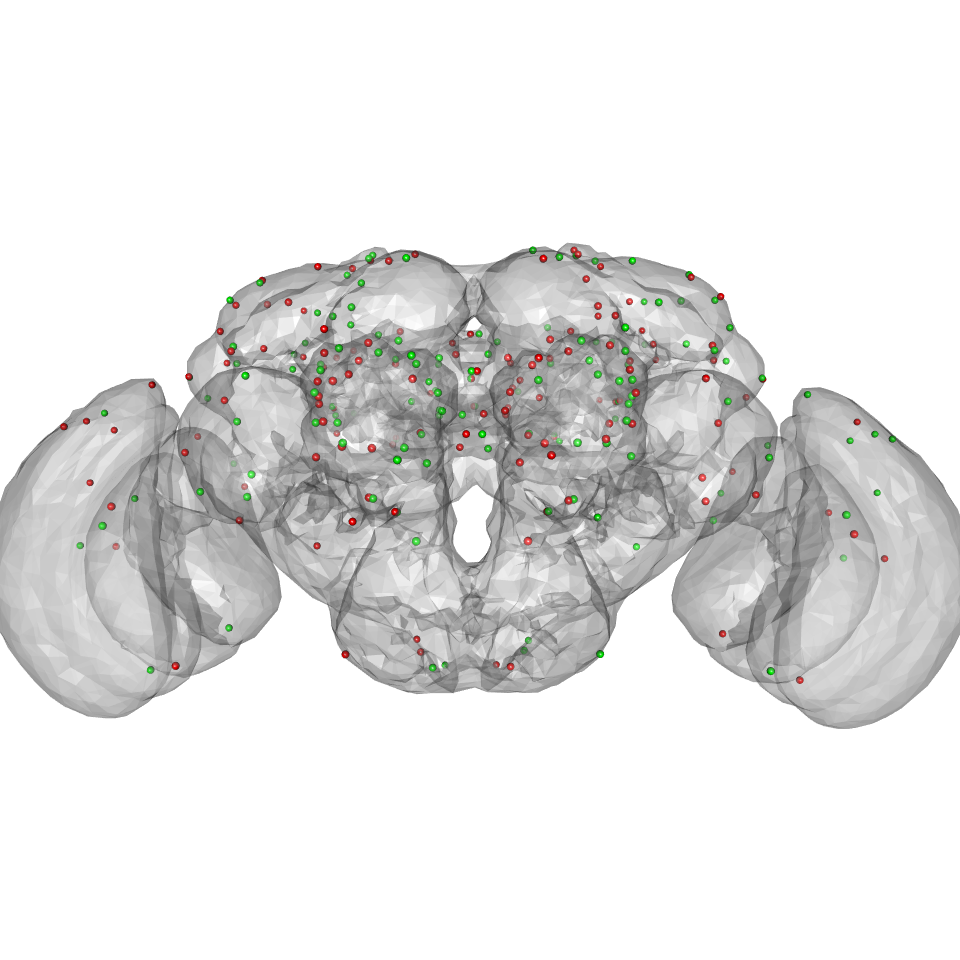
One could then write out a table of landmarks including these mirrored positions like so:
xyzm.pixels=scale(xyzm, scale = voxdims(JFRC2013), center = FALSE) colnames(xyzm.pixels)=c("XM","YM","ZM") write.table(cbind(elm.landmarks, xyzm.pixels), 'elm.landmarks-with-mirror.tsv', col.names = T, sep='\t', row.names = F)
If one were then to take the mirror image landmarks in JFRC2013 space and manually pick the corresponding locations in EM space, one should be able to compare two different paths to the same point (one mirroring in FAFB, the other mirroring in JFRC2013) and see whether there is a difference in the calculated position. Differences would presumably reflect the uncertainty in picking positions in the EM volume (and a small contribution from the mirroring uncertainty in JFRC2013, which nevertheless expect to be <1 µm based on analysis in Manton et al 2014).